The Fascinating Oloid: Parametrization and Surface Area 26-09-2021 geometry math parametrization visualization education
Some geometric shapes captivate not only for their beauty, but also for the unexpected mathematical properties they hide. The oloid , discovered by Paul Schatz in 1929, is one such shape.
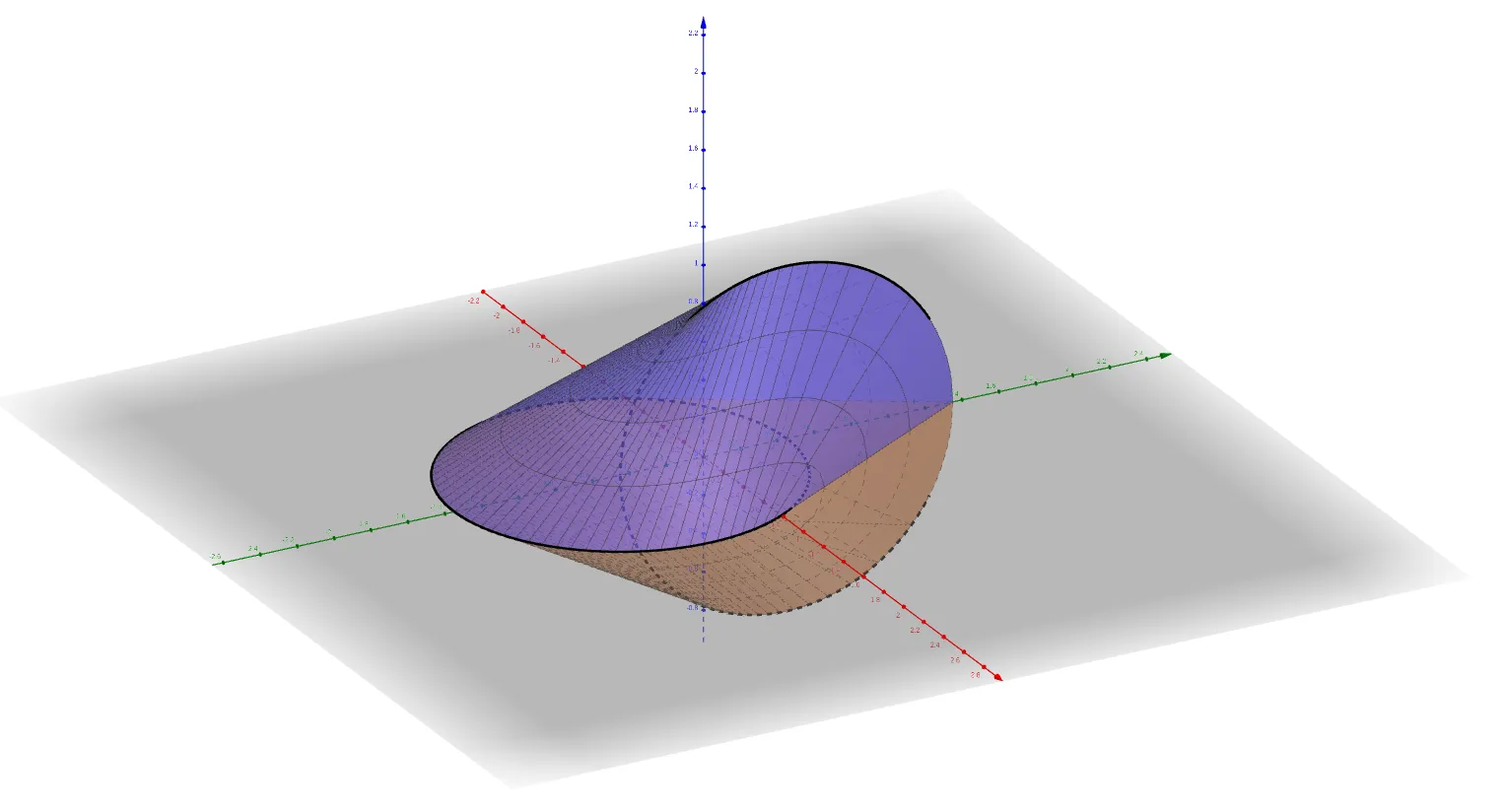
At first glance, it may look like a sculptural curiosity. But the oloid is a ruled surface , generated by line segments between two congruent circles in perpendicular planes, where the center of each lies on the circumference of the other. In this article, weβll explore:
How to define the oloid from two simple circles
How to parameterize its entire surface
Why all generating segments have the same length
And how to compute its surface area β which turns out to be exactly the same as a sphere of radius r r r
Letβs dive in.
From circles to surface
The oloid is generated from two circles:
k a : { x 2 + ( y β r 2 ) 2 = r 2 z = 0 k_a: \begin{cases}
x^2+ \left( y-\frac{r}{2} \right)^2 = r^2 \\
z=0
\end{cases} k a β : { x 2 + ( y β 2 r β ) 2 = r 2 z = 0 β k b : { ( y β r 2 ) 2 + z 2 = r 2 x = 0 k_b: \begin{cases}
\left( y-\frac{r}{2} \right)^2 + z^2 = r^2 \\
x=0
\end{cases} k b β : { ( y β 2 r β ) 2 + z 2 = r 2 x = 0 β These circles lie in perpendicular planes, and the oloid surface is generated by connecting corresponding points from each one.
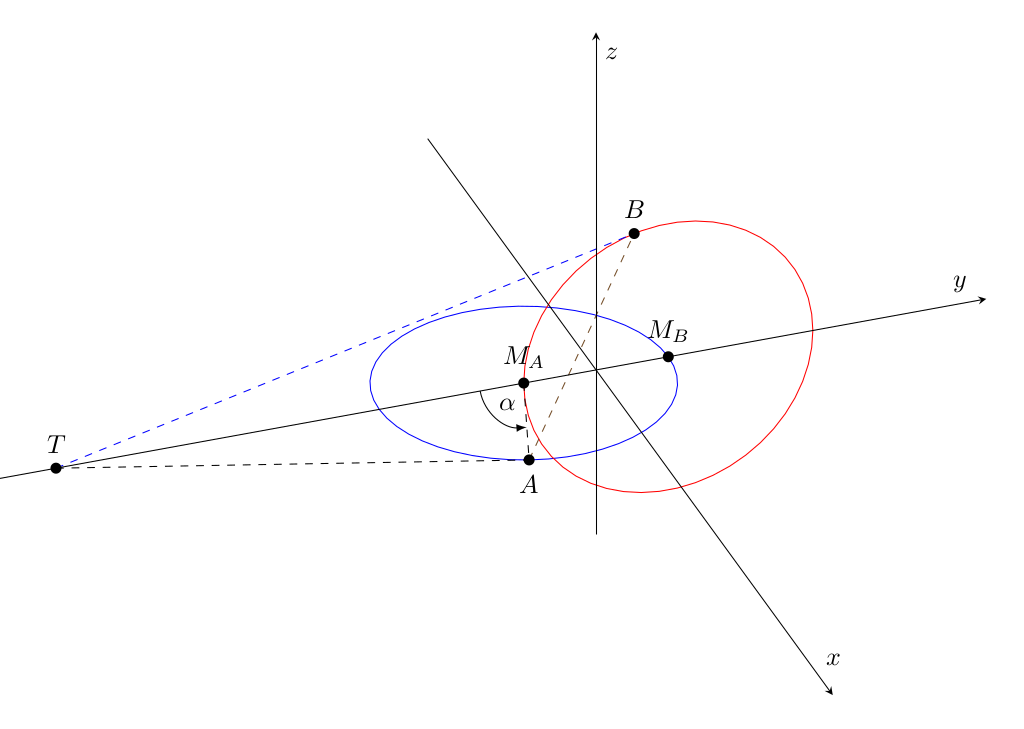
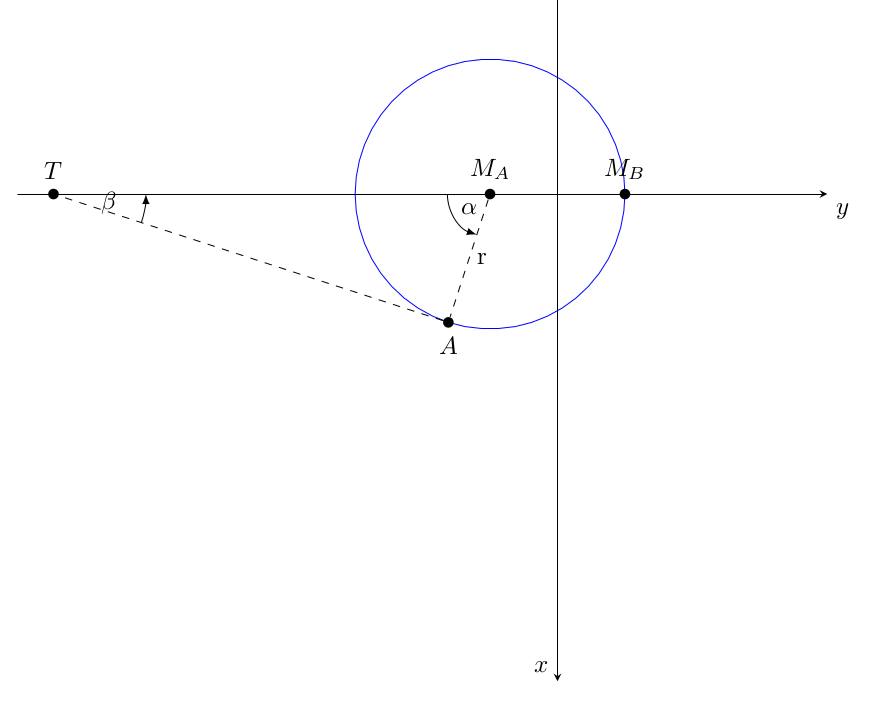
A = ( r β sin β‘ ( Ξ± ) , β r 2 β r β cos β‘ ( Ξ± ) , 0 ) A = \left(\begin{array}{ccc}r\,\sin\left(\alpha\right), & -\dfrac{r}{2}-r\,\cos\left(\alpha\right), & 0 \end{array}\right) A = ( r sin ( Ξ± ) , β β 2 r β β r cos ( Ξ± ) , β 0 β ) Ξ² = Ο β Ξ± / 2 \beta = \pi - \alpha/2 Ξ² = Ο β Ξ± /2 sin β‘ ( Ξ² ) = s i n ( Ο β Ξ± / 2 ) = c o s ( Ξ± ) \sin(\beta) = sin(\pi - \alpha/2) = cos(\alpha) sin ( Ξ² ) = s in ( Ο β Ξ± /2 ) = cos ( Ξ± ) β£ T M A β β£ β sin β‘ ( Ξ² ) = r β
β βΉ β
β β£ T M A β β£ = β£ r cos β‘ ( Ξ± ) β£ |\overrightarrow{\rm TM_A}|\, \sin(\beta) = r \implies |\overrightarrow{\rm TM_A}| = \left| \dfrac{r}{\cos(\alpha)}\right | β£ T M A β β β£ sin ( Ξ² ) = r βΉ β£ T M A β β β£ = β cos ( Ξ± ) r β β T = ( 0 , β r 2 β r cos β‘ ( Ξ± ) , 0 ) T = \left(\begin{array}{ccc} 0, & -\dfrac{r}{2}-\dfrac{r}{\cos\left(\alpha\right)}, & 0 \end{array}\right) T = ( 0 , β β 2 r β β cos ( Ξ± ) r β , β 0 β )
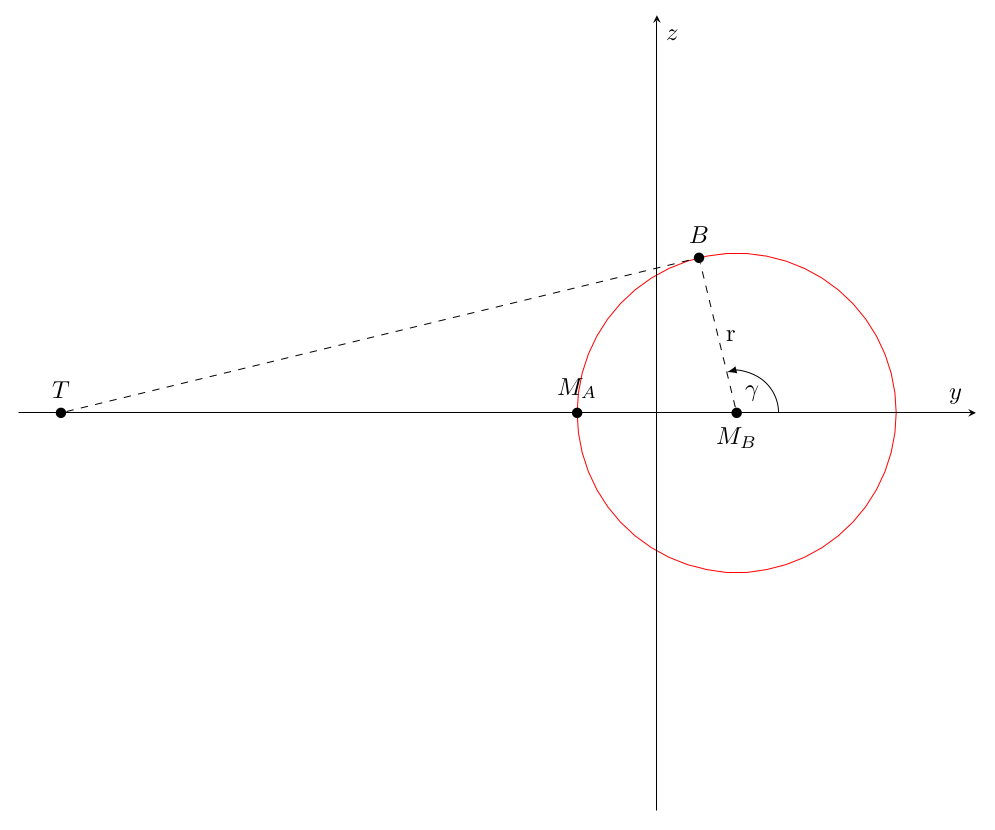
β£ T M B β β£ 2 = β£ T B β β£ 2 + r 2 |\overrightarrow{\rm TM_B}|^2 = |\overrightarrow{\rm TB}|^2 + r^2 β£ T M B β β β£ 2 = β£ TB β£ 2 + r 2 β£ T M B β β£ 2 = ( r 2 + r cos β‘ ( Ξ± ) + r 2 ) 2 = ( r + r Β c o s ( Ξ± ) cos β‘ ( Ξ± ) ) 2 |\overrightarrow{\rm TM_B}|^2 = \left( \dfrac{r}{2}+\dfrac{r}{\cos\left(\alpha\right)}+\dfrac{r}{2} \right)^2 = \left( \dfrac{r + r\ cos(\alpha)}{\cos\left(\alpha\right)} \right)^2 β£ T M B β β β£ 2 = ( 2 r β + cos ( Ξ± ) r β + 2 r β ) 2 = ( cos ( Ξ± ) r + r Β cos ( Ξ± ) β ) 2 cos β‘ ( Ξ³ ) = β r β£ T M B β β£ = β cos β‘ ( Ξ± ) 1 + c o s ( Ξ± ) \cos(\gamma) = \dfrac{-r}{|\overrightarrow{\rm TM_B}|} = \dfrac{-\cos\left(\alpha\right)}{1 + cos(\alpha)} cos ( Ξ³ ) = β£ T M B β β β£ β r β = 1 + cos ( Ξ± ) β cos ( Ξ± ) β B y = r 2 + r Β cos β‘ ( Ξ³ ) = r 2 β r Β cos β‘ ( Ξ± ) 1 + c o s ( Ξ± ) B_y = \dfrac{r}{2}+r\ \cos(\gamma) = \dfrac{r}{2} - \dfrac{r\ \cos\left(\alpha\right)}{1 + cos(\alpha)} B y β = 2 r β + r Β cos ( Ξ³ ) = 2 r β β 1 + cos ( Ξ± ) r Β cos ( Ξ± ) β B z = r Β sin β‘ ( Ξ³ ) B_z = r\ \sin(\gamma) B z β = r Β sin ( Ξ³ ) sin β‘ ( Ξ³ ) 2 = 1 β cos β‘ ( Ξ³ ) 2 = 1 β ( cos β‘ ( Ξ± ) 1 + c o s ( Ξ± ) ) 2 = ( 2 Β cos β‘ ( Ξ± ) + 1 ( cos β‘ ( Ξ± ) + 1 ) 2 ) \sin(\gamma)^2 = 1 - \cos(\gamma)^2 = 1 - \left( \dfrac{\cos\left(\alpha\right)}{1 + cos(\alpha)} \right)^2 = \left( \dfrac{2\ \cos(\alpha) + 1}{(\cos(\alpha) + 1)^2} \right) sin ( Ξ³ ) 2 = 1 β cos ( Ξ³ ) 2 = 1 β ( 1 + cos ( Ξ± ) cos ( Ξ± ) β ) 2 = ( ( cos ( Ξ± ) + 1 ) 2 2 Β cos ( Ξ± ) + 1 β ) B = ( 0 , r 2 β r Β cos β‘ ( Ξ± ) 1 + c o s ( Ξ± ) , Β± Β r β 2 β cos β‘ ( Ξ± ) + 1 cos β‘ ( Ξ± ) + 1 ) B = \left(\begin{array}{ccc} 0, & \dfrac{r}{2} - \dfrac{r\ \cos\left(\alpha\right)}{1 + cos(\alpha)}, & \dfrac{ \pm\ r\,\sqrt{2\,\cos\left(\alpha \right)+1}}{\cos\left(\alpha \right)+1} \end{array}\right) B = ( 0 , β 2 r β β 1 + cos ( Ξ± ) r Β cos ( Ξ± ) β , β cos ( Ξ± ) + 1 Β± Β r 2 cos ( Ξ± ) + 1 β β β ) The square root in the z coordinate of B creates the following restriction:
2 Β cos β‘ ( Ξ± ) + 1 β₯ 0 β
β βΉ β
β β 2 Ο 3 β€ Ξ± β€ 2 Ο 3 2\ \cos(\alpha) + 1 \geq 0 \implies -\dfrac{2 \pi}{3} \leq \alpha \leq \dfrac{2 \pi}{3} 2 Β cos ( Ξ± ) + 1 β₯ 0 βΉ β 3 2 Ο β β€ Ξ± β€ 3 2 Ο β But we have to avoid zero denominators in the y coordinate of B, so the domain of Ξ± \alpha Ξ±
β 2 Ο 3 < Ξ± < 2 Ο 3 -\dfrac{2 \pi}{3} < \alpha < \dfrac{2 \pi}{3} β 3 2 Ο β < Ξ± < 3 2 Ο β What follows is a complete derivation of the parametrization of the oloid, the computation of the length of each generating segment A B β \overrightarrow{AB} A B
Parametrization
We define points A β k a A \in k_a A β k a β B β k b B \in k_b B β k b β Ξ± \alpha Ξ± Ξ± β ( β 2 Ο / 3 , 2 Ο / 3 ) \alpha \in (-2\pi/3, 2\pi/3) Ξ± β ( β 2 Ο /3 , 2 Ο /3 ) v β [ 0 , 1 ] v \in [0,1] v β [ 0 , 1 ]
A + v β
A B β A + v \cdot \overrightarrow{AB} A + v β
A B Click to expand full parametrization A B β = ( β r β sin β‘ ( Ξ± ) , r 2 + r β cos β‘ ( Ξ± ) β r β ( cos β‘ ( Ξ± ) β 1 ) 2 β ( cos β‘ ( Ξ± ) + 1 ) , Β± Β r β 2 β cos β‘ ( Ξ± ) + 1 cos β‘ ( Ξ± ) + 1 ) \overrightarrow{\rm AB} = \left(\begin{array}{ccc} -r\,\sin\left(\alpha \right), & \dfrac{r}{2}+r\,\cos\left(\alpha \right)-\dfrac{r\,\left(\cos\left(\alpha \right)-1\right)}{2\,\left(\cos\left(\alpha \right)+1\right)}, & \dfrac{\pm\ r\,\sqrt{2\,\cos\left(\alpha \right)+1}}{\cos\left(\alpha \right)+1} \end{array}\right) AB = ( β r sin ( Ξ± ) , β 2 r β + r cos ( Ξ± ) β 2 ( cos ( Ξ± ) + 1 ) r ( cos ( Ξ± ) β 1 ) β , β cos ( Ξ± ) + 1 Β± Β r 2 cos ( Ξ± ) + 1 β β β ) A B β = ( β r β sin β‘ ( Ξ± ) , r β ( cos β‘ ( Ξ± ) 2 + cos β‘ ( Ξ± ) + 1 ) cos β‘ ( Ξ± ) + 1 , Β± Β r β 2 β cos β‘ ( Ξ± ) + 1 cos β‘ ( Ξ± ) + 1 ) \overrightarrow{\rm AB} = \left(\begin{array}{ccc} -r\,\sin\left(\alpha \right), & \dfrac{r\,\left({\cos\left(\alpha \right)}^2+\cos\left(\alpha \right)+1\right)}{\cos\left(\alpha \right)+1}, & \dfrac{ \pm\ r\,\sqrt{2\,\cos\left(\alpha \right)+1}}{\cos\left(\alpha \right)+1} \end{array}\right) AB = ( β r sin ( Ξ± ) , β cos ( Ξ± ) + 1 r ( cos ( Ξ± ) 2 + cos ( Ξ± ) + 1 ) β , β cos ( Ξ± ) + 1 Β± Β r 2 cos ( Ξ± ) + 1 β β β ) A + v Β A B β = ( β r β sin β‘ ( Ξ± ) β ( v β 1 ) , r β ( 2 β v β 3 β cos β‘ ( Ξ± ) β 2 β cos β‘ ( Ξ± ) 2 + 2 β v β cos β‘ ( Ξ± ) + 2 β v β cos β‘ ( Ξ± ) 2 β 1 ) 2 β ( cos β‘ ( Ξ± ) + 1 ) , Β± Β r β v β 2 β cos β‘ ( Ξ± ) + 1 cos β‘ ( Ξ± ) + 1 ) A + v\ \overrightarrow{\rm AB} = \left(\begin{array}{ccc} -r\,\sin\left(\alpha \right)\,\left(v-1\right), & \dfrac{r\,\left(2\,v-3\,\cos\left(\alpha \right)-2\,{\cos\left(\alpha \right)}^2+2\,v\,\cos\left(\alpha \right)+2\,v\,{\cos\left(\alpha \right)}^2-1\right)}{2\,\left(\cos\left(\alpha \right)+1\right)}, & \dfrac{\pm\ r\,v\,\sqrt{2\,\cos\left(\alpha \right)+1}}{\cos\left(\alpha \right)+1} \end{array}\right) A + v Β AB = ( β r sin ( Ξ± ) ( v β 1 ) , β 2 ( cos ( Ξ± ) + 1 ) r ( 2 v β 3 cos ( Ξ± ) β 2 cos ( Ξ± ) 2 + 2 v cos ( Ξ± ) + 2 v cos ( Ξ± ) 2 β 1 ) β , β cos ( Ξ± ) + 1 Β± Β r v 2 cos ( Ξ± ) + 1 β β β ) 0 β€ v β€ 1 , Β β 2 Ο 3 < Ξ± < 2 Ο 3 0 \leq v \leq 1,\ -\dfrac{2 \pi}{3} < \alpha < \dfrac{2 \pi}{3} 0 β€ v β€ 1 , Β β 3 2 Ο β < Ξ± < 3 2 Ο β Proving that all AB segments length is constant for all Ξ± \alpha Ξ±
β£ A B β β£ 2 = r 2 Β sin β‘ ( Ξ± ) 2 + r 2 β ( cos β‘ ( Ξ± ) 2 + cos β‘ ( Ξ± ) + 1 ) 2 ( cos β‘ ( Ξ± ) + 1 ) 2 + r 2 β ( 2 β cos β‘ ( Ξ± ) + 1 ) ( cos β‘ ( Ξ± ) + 1 ) 2 |\overrightarrow{\rm AB}|^2 = r^2\ \sin(\alpha)^2 + \dfrac{r^2\,\left({\cos\left(\alpha \right)}^2+\cos\left(\alpha \right)+1\right)^2}{(\cos\left(\alpha \right)+1)^2} + \dfrac{r^2\,(2\,\cos\left(\alpha \right)+1)}{(\cos\left(\alpha \right)+1)^2} β£ AB β£ 2 = r 2 Β sin ( Ξ± ) 2 + ( cos ( Ξ± ) + 1 ) 2 r 2 ( cos ( Ξ± ) 2 + cos ( Ξ± ) + 1 ) 2 β + ( cos ( Ξ± ) + 1 ) 2 r 2 ( 2 cos ( Ξ± ) + 1 ) β Click to expand full derivation β£ A B β β£ 2 = r 2 β ( 1 β cos β‘ ( Ξ± ) 2 + ( cos β‘ ( Ξ± ) 2 + cos β‘ ( Ξ± ) + 1 ) 2 ( cos β‘ ( Ξ± ) + 1 ) 2 + 2 β cos β‘ ( Ξ± ) + 1 ( cos β‘ ( Ξ± ) + 1 ) 2 ) |\overrightarrow{\rm AB}|^2 = r^2\,\left(1 -{\cos\left(\alpha \right)}^2+\frac{{\left({\cos\left(\alpha \right)}^2+\cos\left(\alpha \right)+1\right)}^2}{{\left(\cos\left(\alpha \right)+1\right)}^2} + \frac{2\,\cos\left(\alpha \right)+1}{{\left(\cos\left(\alpha \right)+1\right)}^2}\right) β£ AB β£ 2 = r 2 β 1 β cos ( Ξ± ) 2 + ( cos ( Ξ± ) + 1 ) 2 ( cos ( Ξ± ) 2 + cos ( Ξ± ) + 1 ) 2 β + ( cos ( Ξ± ) + 1 ) 2 2 cos ( Ξ± ) + 1 β β t = cos β‘ ( Ξ± ) t = \cos(\alpha) t = cos ( Ξ± ) β£ A B β β£ 2 = r 2 β ( 1 β t 2 + ( t 2 + t + 1 ) 2 ( t + 1 ) 2 + 2 β t + 1 ( t + 1 ) 2 ) |\overrightarrow{\rm AB}|^2 = r^2\,\left(1-t^2+\frac{{\left(t^2+t+1\right)}^2}{{\left(t+1\right)}^2}+\frac{2\,t+1}{{\left(t+1\right)}^2}\right) β£ AB β£ 2 = r 2 ( 1 β t 2 + ( t + 1 ) 2 ( t 2 + t + 1 ) 2 β + ( t + 1 ) 2 2 t + 1 β ) β£ A B β β£ 2 = r 2 β ( ( 1 β t 2 ) ( t + 1 ) 2 + ( t 2 + t + 1 ) 2 + ( 2 t + 1 ) ( t + 1 ) 2 ) |\overrightarrow{\rm AB}|^2 = r^2\,\left( \dfrac{(1-t^2)(t+1)^2+(t^2+t+1)^2+(2t+1)}{(t+1)^2} \right) β£ AB β£ 2 = r 2 ( ( t + 1 ) 2 ( 1 β t 2 ) ( t + 1 ) 2 + ( t 2 + t + 1 ) 2 + ( 2 t + 1 ) β ) β£ A B β β£ 2 = r 2 β ( 3 t 2 + 6 t + 3 ( t + 1 ) 2 ) |\overrightarrow{\rm AB}|^2 = r^2\,\left( \dfrac{3t^2 + 6t + 3}{(t+1)^2} \right) β£ AB β£ 2 = r 2 ( ( t + 1 ) 2 3 t 2 + 6 t + 3 β ) β£ A B β β£ 2 = r 2 β ( 3 Β ( t + 1 ) 2 ( t + 1 ) 2 ) |\overrightarrow{\rm AB}|^2 = r^2\,\left( \dfrac{3\ (t+1)^2}{(t+1)^2} \right) β£ AB β£ 2 = r 2 ( ( t + 1 ) 2 3 Β ( t + 1 ) 2 β ) β£ A B β β£ 2 = 3 r 2 |\overrightarrow{\rm AB}|^2 = 3r^2 β£ AB β£ 2 = 3 r 2 β£ A B β β£ = 3 Β r |\overrightarrow{\rm AB}| = \sqrt3 \ r β£ AB β£ = 3 β Β r Meaning all segments have equal length β a surprisingly symmetric property.
Surface area of the oloid
Because the oloid is a ruled surface, we apply a surface area formula adapted from J. B. Reynolds (source ).
A = β« Ξ± 1 Ξ± 2 β« v 1 v 2 β£ A B β Γ ( ( 1 β v ) Β d Β O B β d Ξ± + v Β d Β O A β d Ξ± ) β£ β d Ξ± Β d v A = \int_{\alpha_1}^{\alpha_2} \int_{v_1}^{v_2} \left| \overrightarrow{\rm AB} \times \left((1-v)\ \frac{d \ \overrightarrow{OB}}{d\alpha} + v\ \frac{d \ \overrightarrow{OA}}{d\alpha} \right) \right| \,d\alpha\ dv A = β« Ξ± 1 β Ξ± 2 β β β« v 1 β v 2 β β β AB Γ ( ( 1 β v ) Β d Ξ± d Β OB β + v Β d Ξ± d Β O A β ) β d Ξ± Β d v A = β« β 2 Ο / 3 2 Ο / 3 β« 0 1 β£ A B β Γ ( ( 1 β v ) Β d β O B β d Ξ± + v Β d β O A β d Ξ± ) β£ β d Ξ± β d v A = \int_{-2\pi/3}^{2\pi/3} \int_{0}^{1} \left| \overrightarrow{\rm AB} \times \left((1-v)\ \frac{d\,\overrightarrow{OB}}{d\alpha} + v\ \frac{d\,\overrightarrow{OA}}{d\alpha} \right) \right| \,d\alpha\, dv A = β« β 2 Ο /3 2 Ο /3 β β« 0 1 β β AB Γ ( ( 1 β v ) Β d Ξ± d OB β + v Β d Ξ± d O A β ) β d Ξ± d v d Β O B β d Β Ξ± = ( 0 , r β sin β‘ ( Ξ± ) ( cos β‘ ( Ξ± ) + 1 ) 2 , Β± Β r β sin β‘ ( 2 β Ξ± ) 2 β ( cos β‘ ( Ξ± ) + 1 ) 2 β 2 β cos β‘ ( Ξ± ) + 1 ) \frac{d \ \overrightarrow{OB}}{d \ \alpha} = \left(\begin{array}{ccc} 0, & \dfrac{r\,\sin\left(\alpha \right)}{{\left(\cos\left(\alpha \right)+1\right)}^2}, & \dfrac{\pm\ r\,\sin\left(2\,\alpha \right)}{2\,{\left(\cos\left(\alpha \right)+1\right)}^2\,\sqrt{2\,\cos\left(\alpha \right)+1}} \end{array}\right) d Β Ξ± d Β OB β = ( 0 , β ( cos ( Ξ± ) + 1 ) 2 r sin ( Ξ± ) β , β 2 ( cos ( Ξ± ) + 1 ) 2 2 cos ( Ξ± ) + 1 β Β± Β r sin ( 2 Ξ± ) β β ) d Β O A β d Β Ξ± = ( r β cos β‘ ( Ξ± ) , r β sin β‘ ( Ξ± ) , 0 ) \frac{d \ \overrightarrow{OA}}{d \ \alpha} = \left(\begin{array}{ccc} r\,\cos\left(\alpha \right), & r\,\sin\left(\alpha \right), & 0 \end{array}\right) d Β Ξ± d Β O A β = ( r cos ( Ξ± ) , β r sin ( Ξ± ) , β 0 β ) Click to expand full derivation Since weβll continue with the positive value of the 3rd coordinate of the derivative of OB, we are computing the oloidβs top surface. Then, in order to have the total surface, weβll have to multiply by 2 the result of the integral.
( 1 β v ) Β d Β O B β Ξ± + v Β d Β O A β Ξ± = ( r β v β cos β‘ ( Ξ± ) , r β sin β‘ ( Ξ± ) β ( v β cos β‘ ( Ξ± ) 2 + 2 β v β cos β‘ ( Ξ± ) + 1 ) ( cos β‘ ( Ξ± ) + 1 ) 2 , β r β sin β‘ ( 2 β Ξ± ) β ( v β 1 ) 2 β ( cos β‘ ( Ξ± ) + 1 ) 2 β 2 β cos β‘ ( Ξ± ) + 1 ) (1-v)\ \frac{d \ \overrightarrow{OB}}{\alpha} + v\ \frac{d \ \overrightarrow{OA}}{\alpha} = \left(\begin{array}{ccc} r\,v\,\cos\left(\alpha \right), & \dfrac{r\,\sin\left(\alpha \right)\,\left(v\,{\cos\left(\alpha \right)}^2+2\,v\,\cos\left(\alpha \right)+1\right)}{{\left(\cos\left(\alpha \right)+1\right)}^2}, & -\dfrac{r\,\sin\left(2\,\alpha \right)\,\left(v-1\right)}{2\,{\left(\cos\left(\alpha \right)+1\right)}^2\,\sqrt{2\,\cos\left(\alpha \right)+1}} \end{array}\right) ( 1 β v ) Β Ξ± d Β OB β + v Β Ξ± d Β O A β = β r v cos ( Ξ± ) , β ( cos ( Ξ± ) + 1 ) 2 r sin ( Ξ± ) ( v cos ( Ξ± ) 2 + 2 v cos ( Ξ± ) + 1 ) β , β β 2 ( cos ( Ξ± ) + 1 ) 2 2 cos ( Ξ± ) + 1 β r sin ( 2 Ξ± ) ( v β 1 ) β β β A B β Γ ( ( 1 β v ) Β d Β O B β Ξ± + v Β d Β O A β Ξ± ) = \overrightarrow{\rm AB} \times \left((1-v)\ \frac{d \ \overrightarrow{OB}}{\alpha} + v\ \frac{d \ \overrightarrow{OA}}{\alpha} \right) = AB Γ ( ( 1 β v ) Β Ξ± d Β OB β + v Β Ξ± d Β O A β ) = = ( β r 2 β sin β‘ ( Ξ± ) β ( 3 β v β cos β‘ ( Ξ± ) β cos β‘ ( Ξ± ) + 1 ) ( cos β‘ ( Ξ± ) + 1 ) β 2 β cos β‘ ( Ξ± ) + 1 , r 2 β cos β‘ ( Ξ± ) β ( 3 β v β cos β‘ ( Ξ± ) β cos β‘ ( Ξ± ) + 1 ) ( cos β‘ ( Ξ± ) + 1 ) β 2 β cos β‘ ( Ξ± ) + 1 , β r 2 β ( 3 β v β cos β‘ ( Ξ± ) β cos β‘ ( Ξ± ) + 1 ) cos β‘ ( Ξ± ) + 1 ) = \left(\begin{array}{ccc} -\dfrac{r^2\,\sin\left(\alpha \right)\,\left(3\,v\,\cos\left(\alpha \right)-\cos\left(\alpha \right)+1\right)}{\left(\cos\left(\alpha \right)+1\right)\,\sqrt{2\,\cos\left(\alpha \right)+1}}, & \dfrac{r^2\,\cos\left(\alpha \right)\,\left(3\,v\,\cos\left(\alpha \right)-\cos\left(\alpha \right)+1\right)}{\left(\cos\left(\alpha \right)+1\right)\,\sqrt{2\,\cos\left(\alpha \right)+1}}, & -\dfrac{r^2\,\left(3\,v\,\cos\left(\alpha \right)-\cos\left(\alpha \right)+1\right)}{\cos\left(\alpha \right)+1} \end{array}\right) = ( β ( cos ( Ξ± ) + 1 ) 2 cos ( Ξ± ) + 1 β r 2 sin ( Ξ± ) ( 3 v cos ( Ξ± ) β cos ( Ξ± ) + 1 ) β , β ( cos ( Ξ± ) + 1 ) 2 cos ( Ξ± ) + 1 β r 2 cos ( Ξ± ) ( 3 v cos ( Ξ± ) β cos ( Ξ± ) + 1 ) β , β β cos ( Ξ± ) + 1 r 2 ( 3 v cos ( Ξ± ) β cos ( Ξ± ) + 1 ) β β ) β£ A B β Γ ( ( 1 β v ) Β d Β O B β Ξ± + v Β d Β O A β Ξ± ) β£ 2 = 2 β r 4 β ( 3 β v β cos β‘ ( Ξ± ) β cos β‘ ( Ξ± ) + 1 ) 2 2 β cos β‘ ( Ξ± ) 2 + 3 β cos β‘ ( Ξ± ) + 1 \left| \overrightarrow{\rm AB} \times \left((1-v)\ \frac{d \ \overrightarrow{OB}}{\alpha} + v\ \frac{d \ \overrightarrow{OA}}{\alpha} \right) \right|^2 = \frac{2\,r^4\,{\left(3\,v\,\cos\left(\alpha \right)-\cos\left(\alpha \right)+1\right)}^2}{2\,{\cos\left(\alpha \right)}^2+3\,\cos\left(\alpha \right)+1} β AB Γ ( ( 1 β v ) Β Ξ± d Β OB β + v Β Ξ± d Β O A β ) β 2 = 2 cos ( Ξ± ) 2 + 3 cos ( Ξ± ) + 1 2 r 4 ( 3 v cos ( Ξ± ) β cos ( Ξ± ) + 1 ) 2 β A = 2 Β 2 Β r 2 β« β 2 Ο / 3 2 Ο / 3 β« 0 1 3 β v β cos β‘ ( Ξ± ) β cos β‘ ( Ξ± ) + 1 2 β cos β‘ ( Ξ± ) 2 + 3 β cos β‘ ( Ξ± ) + 1 β d Ξ± Β d v A =2 \ \sqrt{2} \ r^2 \int_{-2\pi/3}^{2\pi/3} \int_{0}^{1} \frac{{3\,v\,\cos\left(\alpha \right)-\cos\left(\alpha \right)+1}}{\sqrt{2\,{\cos\left(\alpha \right)}^2+3\,\cos\left(\alpha \right)+1}} \,d\alpha\ dv A = 2 Β 2 β Β r 2 β« β 2 Ο /3 2 Ο /3 β β« 0 1 β 2 cos ( Ξ± ) 2 + 3 cos ( Ξ± ) + 1 β 3 v cos ( Ξ± ) β cos ( Ξ± ) + 1 β d Ξ± Β d v A = 2 2 β r 2 β« β 2 Ο / 3 2 Ο / 3 1 2 cos β‘ ( Ξ± ) + 1 2 cos β‘ 2 ( Ξ± ) + 3 cos β‘ ( Ξ± ) + 1 β d Ξ± A = 2 \sqrt{2} \, r^2 \int_{-2\pi/3}^{2\pi/3} \frac{\tfrac{1}{2} \cos(\alpha) + 1}{\sqrt{2 \cos^2(\alpha) + 3 \cos(\alpha) + 1}} \, d\alpha A = 2 2 β r 2 β« β 2 Ο /3 2 Ο /3 β 2 cos 2 ( Ξ± ) + 3 cos ( Ξ± ) + 1 β 2 1 β cos ( Ξ± ) + 1 β d Ξ± A = 2 Β 2 Β r 2 Β cos β‘ ( Ξ± 2 ) 2 Β cos β‘ ( Ξ± ) + 1 ( sin β‘ β 1 ( 2 sin β‘ ( Ξ± 2 ) 3 ) + tan β‘ β 1 ( sin β‘ ( Ξ± 2 ) 2 Β cos β‘ Ξ± + 1 ) ) 2 β cos β‘ ( Ξ± ) 2 + 3 β cos β‘ ( Ξ± ) + 1 β£ β 2 Ο / 3 2 Ο / 3 A =\left. 2 \ \sqrt{2} \ r^2 \ \dfrac{\cos\left(\dfrac{\alpha}{2}\right) \sqrt{2\ \cos(\alpha) + 1} \left( \sin^{-1}\left( \dfrac{2 \sin\left( \dfrac{\alpha}{2}\right)}{\sqrt{3}}\right) + \tan^{-1} \left( \dfrac{\sin\left(\dfrac{\alpha}{2} \right)}{\sqrt{2\ \cos{\alpha} + 1} } \right)\right)}{\sqrt{2\,{\cos\left(\alpha \right)}^2+3\,\cos\left(\alpha \right)+1}} \right|_{-2\pi/3}^{2\pi/3} A = 2 Β 2 β Β r 2 Β 2 cos ( Ξ± ) 2 + 3 cos ( Ξ± ) + 1 β cos ( 2 Ξ± β ) 2 Β cos ( Ξ± ) + 1 β β sin β 1 β 3 β 2 sin ( 2 Ξ± β ) β β + tan β 1 β 2 Β cos Ξ± + 1 β sin ( 2 Ξ± β ) β β β β β β 2 Ο /3 2 Ο /3 β A = 2 Β 2 Β r 2 Β cos β‘ ( Ξ± 2 ) 2 Β cos β‘ ( Ξ± ) + 1 ( sin β‘ β 1 ( 2 sin β‘ ( Ξ± 2 ) 3 ) + tan β‘ β 1 ( sin β‘ ( Ξ± 2 ) 2 Β cos β‘ Ξ± + 1 ) ) ( 2 Β cos β‘ ( Ξ± ) + 1 ) ( cos β‘ ( Ξ± ) + 1 ) β£ β 2 Ο / 3 2 Ο / 3 A =\left. 2 \ \sqrt{2} \ r^2 \ \dfrac{\cos\left(\dfrac{\alpha}{2}\right) \sqrt{2\ \cos(\alpha) + 1} \left( \sin^{-1}\left( \dfrac{2 \sin\left( \dfrac{\alpha}{2}\right)}{\sqrt{3}}\right) + \tan^{-1} \left( \dfrac{\sin\left(\dfrac{\alpha}{2} \right)}{\sqrt{2\ \cos{\alpha} + 1} } \right)\right)}{\sqrt{(2\ \cos(\alpha) + 1)(\cos(\alpha) + 1)}} \right|_{-2\pi/3}^{2\pi/3} A = 2 Β 2 β Β r 2 Β ( 2 Β cos ( Ξ± ) + 1 ) ( cos ( Ξ± ) + 1 ) β cos ( 2 Ξ± β ) 2 Β cos ( Ξ± ) + 1 β β sin β 1 β 3 β 2 sin ( 2 Ξ± β ) β β + tan β 1 β 2 Β cos Ξ± + 1 β sin ( 2 Ξ± β ) β β β β β β 2 Ο /3 2 Ο /3 β A = 2 Β 2 Β r 2 Β cos β‘ ( Ξ± 2 ) ( sin β‘ β 1 ( 2 sin β‘ ( Ξ± 2 ) 3 ) + tan β‘ β 1 ( sin β‘ ( Ξ± 2 ) 2 Β cos β‘ Ξ± + 1 ) ) cos β‘ ( Ξ± ) + 1 β£ β 2 Ο / 3 2 Ο / 3 A =\left. 2 \ \sqrt{2} \ r^2 \ \dfrac{\cos\left(\dfrac{\alpha}{2}\right) \left( \sin^{-1}\left( \dfrac{2 \sin\left( \dfrac{\alpha}{2}\right)}{\sqrt{3}}\right) + \tan^{-1} \left( \dfrac{\sin\left(\dfrac{\alpha}{2} \right)}{\sqrt{2\ \cos{\alpha} + 1} } \right)\right)}{\sqrt{\cos(\alpha) + 1}} \right|_{-2\pi/3}^{2\pi/3} A = 2 Β 2 β Β r 2 Β cos ( Ξ± ) + 1 β cos ( 2 Ξ± β ) β sin β 1 β 3 β 2 sin ( 2 Ξ± β ) β β + tan β 1 β 2 Β cos Ξ± + 1 β sin ( 2 Ξ± β ) β β β β β β 2 Ο /3 2 Ο /3 β A = 2 Β 2 Β r 2 ( 2 Ο 2 + 2 Ο 2 ) = 2 Β 2 Β r 2 ( 2 Β Ο ) = 4 Β Ο Β r 2 A =2 \ \sqrt{2} \ r^2 \left( \dfrac{\sqrt{2} \pi}{2} + \dfrac{\sqrt{2} \pi}{2} \right) = 2 \ \sqrt{2} \ r^2 \left( \sqrt{2}\ \pi \right) = 4\ \pi \ r^2 A = 2 Β 2 β Β r 2 ( 2 2 β Ο β + 2 2 β Ο β ) = 2 Β 2 β Β r 2 ( 2 β Β Ο ) = 4 Β Ο Β r 2 Through careful differentiation and vector cross products, we derive the integral that gives the total surface. After evaluating the integral (included in full in the article), we obtain:
A = 4 Ο r 2 A = 4\pi r^2 A = 4 Ο r 2 Exactly the same surface area as a sphere of radius r r r
Explore interactively
You can find a parametrized oloid in this GeoGebra link .
