
Resolviendo el problema del viajante (TSP) con C# y AutoCAD
TSP optimización algoritmos AutoCAD programación
El Problema del Viajante (TSP) es un clásico en la computación y la optimización, planteado de la siguiente manera:
Dada una lista de ciudades y las distancias entre cada par de ellas, ¿cuál es la ruta más corta que visita cada ciudad exactamente una vez y regresa a la ciudad de origen?
A pesar de lo simple que es describirlo —¡hasta un niño lo entendería!—, aún no existe un algoritmo eficiente que garantice la solución óptima. Es un problema clasificado como NP-Hard, lo que significa que no se ha encontrado un algoritmo de tiempo polinomial para resolverlo en todos los casos. Como veremos, una computadora moderna puede encontrar la solución exacta solo hasta aproximadamente 22-24 nodos.
Me resulta inspirador que hoy, con todo nuestro avance tecnológico, sigan existiendo problemas tan sencillos de entender… ¡y tan difíciles de resolver! No hablamos de física cuántica o dinámica de fluidos: solo queremos encontrar la ruta más corta entre unos puntos.
En este artículo vamos a:
- Implementar distintos algoritmos que resuelven el TSP de forma óptima y aproximada.
- Programarlos en C#.
- Integrarlos como un plugin de AutoCAD con interfaz gráfica amigable.
✨ Interfaz del plugin
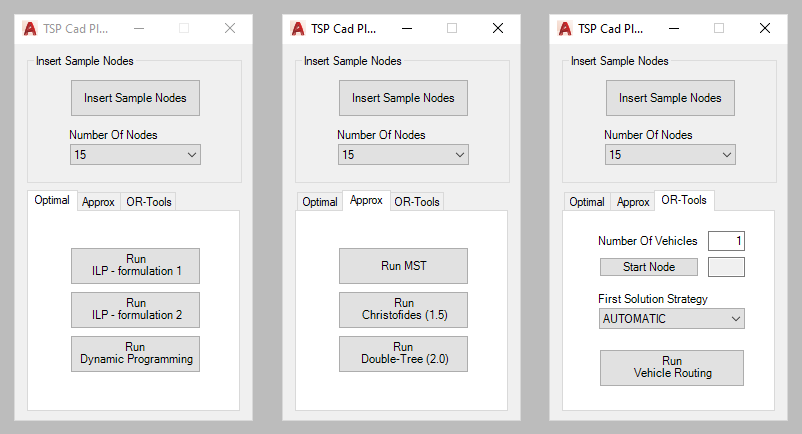
El plugin cuenta con una interfaz en forma de ventana con pestañas, desde donde se puede:
- Insertar nodos de ejemplo en el modelo CAD.
- Seleccionar un algoritmo.
- Resolver y visualizar la ruta óptima.
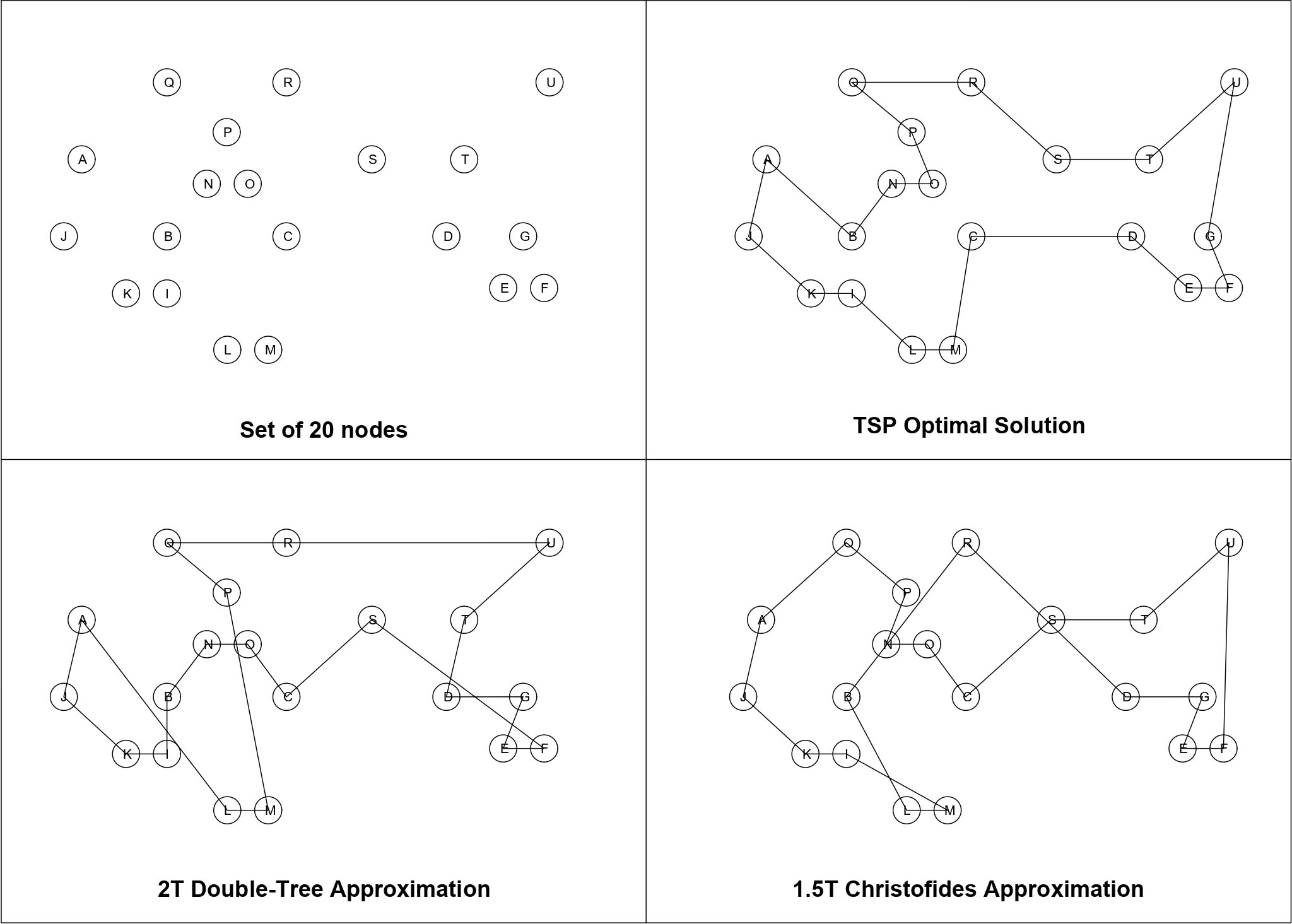
Por ejemplo, se pueden insertar 20 nodos y aplicar un algoritmo:
🧠 Introducción a los algoritmos TSP
La solución más ingenua es la fuerza bruta: probar todas las rutas posibles. Su complejidad es (O(n!)), exactamente ((n-1)!/2), considerando rutas simétricas. Es decir, 1 → 2 → 3 → 1 es equivalente a 1 → 3 → 2 → 1.
Como esto no escala bien, en este artículo exploramos:
-
🧮 Dos métodos para solución óptima:
- Programación Lineal Entera (ILP)
- Programación Dinámica (DP)
-
🌀 Dos algoritmos de aproximación:
- Double Tree (2T)
- Christofides (1.5T)
-
🚀 Finalmente, el uso de Google OR-Tools, una librería gratuita de optimización combinatoria muy poderosa.
🔍 Soluciones óptimas
Explicamos con profundidad:
- Cómo modelar el problema TSP como un problema de programación lineal.
- Dos formas de eliminar subtours: mediante subconjuntos o usando variables de tiempo (Miller–Tucker–Zemlin).
- Cómo programarlo en C# usando Google OR-Tools.
También implementamos el enfoque de programación dinámica con memoización y bottom-up, usando la recurrencia clásica para TSP:
Comparando tiempos:
| 3 | 6 | 72 |
| 4 | 24 | 256 |
| 5 | 120 | 800 |
| 6 | 720 | 2,304 |
| 7 | 5,040 | 6,272 |
| 8 | 40,320 | 16,384 |
| 9 | 362,880 | 41,472 |
| 10 | 3,628,800 | 102,400 |
| 11 | 39,916,800 | 247,808 |
| 12 | 479,001,600 | 589,824 |
| 13 | 6,227,020,800 | 1,384,448 |
| 14 | 87,178,291,200 | 3,211,264 |
| 15 | 1,307,674,368,000 | 7,372,800 |
⚖️ Algoritmos de aproximación
Dado que los métodos óptimos no escalan, recurrimos a aproximaciones:
🌲 Double-Tree (2T)
Pasos:
- Obtener un Árbol Recubridor Mínimo (MST)
- Duplicar todas sus aristas
- Buscar un ciclo Euleriano
- Acortar el recorrido removiendo nodos duplicados
Worst-case: 2x óptimo
🔄 Christofides (1.5T)
Pasos:
- MST
- Obtener nodos de grado impar (S)
- Hallar el emparejamiento perfecto mínimo (en S)
- Unir con el MST → Grafo Euleriano
- Encontrar tour Euleriano y acortarlo
Worst-case: 1.5x óptimo
🛠️ Google OR-Tools
OR-Tools ofrece una potente implementación del TSP con estrategias como:
CHRISTOFIDESPATH_CHEAPEST_ARCGLOBAL_CHEAPEST_ARC
Ejemplo con 50 nodos y distintas estrategias:
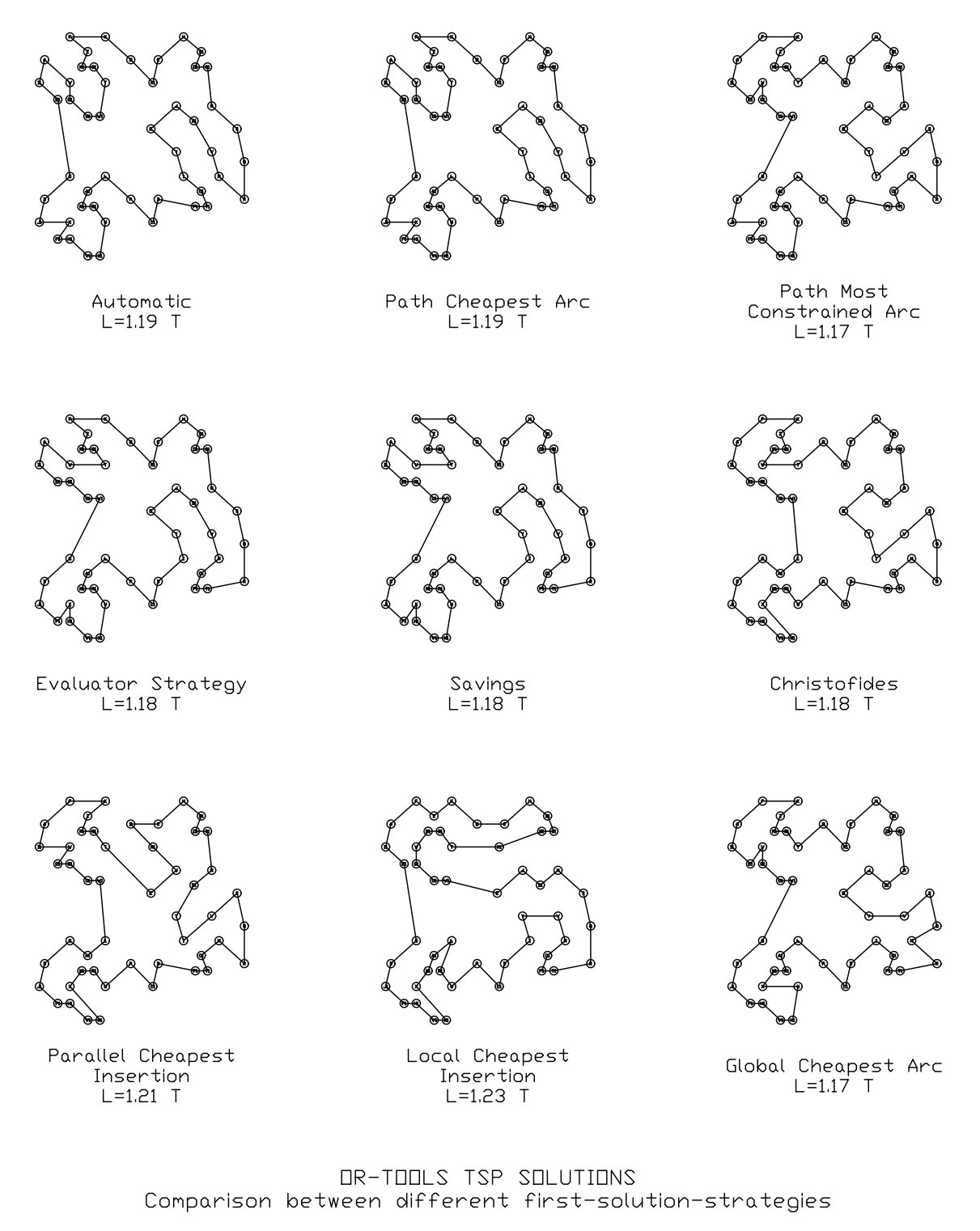
Con 500 nodos: solución en 3.19 s. Con 1,000 nodos: 13.47 s. ¡Nada mal!
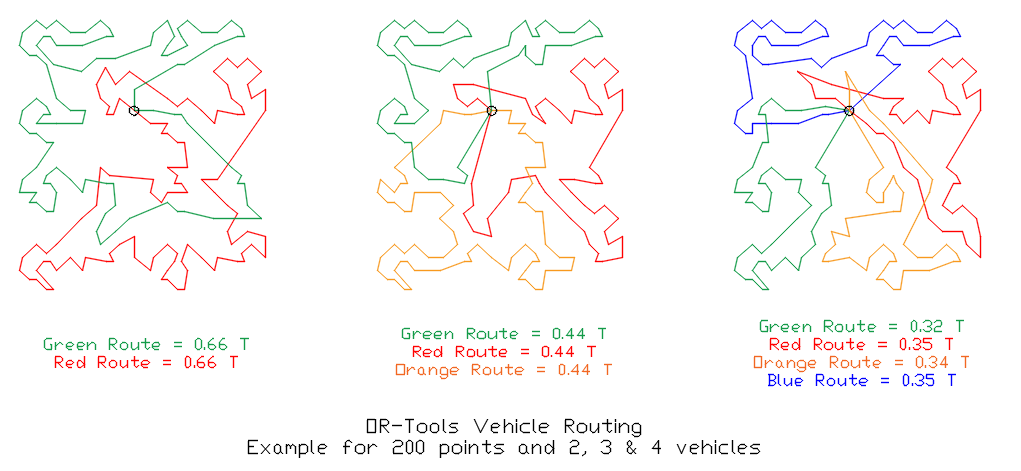
Además, OR-Tools permite resolver problemas de rutas de vehículos (VRP), una extensión natural del TSP.
📦 Código fuente
El código completo está disponible en este repositorio de GitHub.
Si te gustó este artículo, por favor dale a 👏 y compártelo. Puedes seguirme en mi LinkedIn, Twitter, Facebook o Medium.
¡Gracias por leer!