Compartir un secreto con interpolación polinómica
cryptography math programming javascript education
Siempre he creído que la programación y las matemáticas hacen una muy buena combinación. Aunque no me considero un experto en ninguna de las dos áreas, disfruto mucho aprendiendo sobre ellas. Suelo visitar Hacker News, donde a veces encuentro artículos realmente fascinantes. No hace mucho, me topé con un enlace al libro A Programmer’s Introduction to Mathematics de Jeremy Kun, un excelente libro que utiliza programación para ayudar a los lectores a comprender conceptos matemáticos a través de ejemplos prácticos.
El primer capítulo trata sobre polinomios. Aunque estudié álgebra en la universidad, nunca había abordado este tema de la forma en que lo presenta el libro. No conocía la interpolación polinómica ni su aplicación en la criptografía.
Jeremy explica cómo compartir un número secreto usando interpolación polinómica, basado en el artículo original “How To Share a Secret” de Adi Shamir.
Uno de los ejercicios del libro propone crear una aplicación web que use este mecanismo para que los usuarios puedan generar un número secreto y compartirlo con personas específicas. Al encontrar este ejercicio, me pareció completamente inalcanzable. Había hecho cursos de Node, React, bases de datos, algoritmos, estructuras de datos… (por cierto, recomiendo mucho Zero To Mastery Academy), pero nunca había creado una app web completa por mi cuenta. Este ejercicio me empujó a intentarlo y me permitió aplicar conocimientos matemáticos que no comprendía del todo. A continuación, explico el proceso y el código que utilicé.
Fundamento matemático
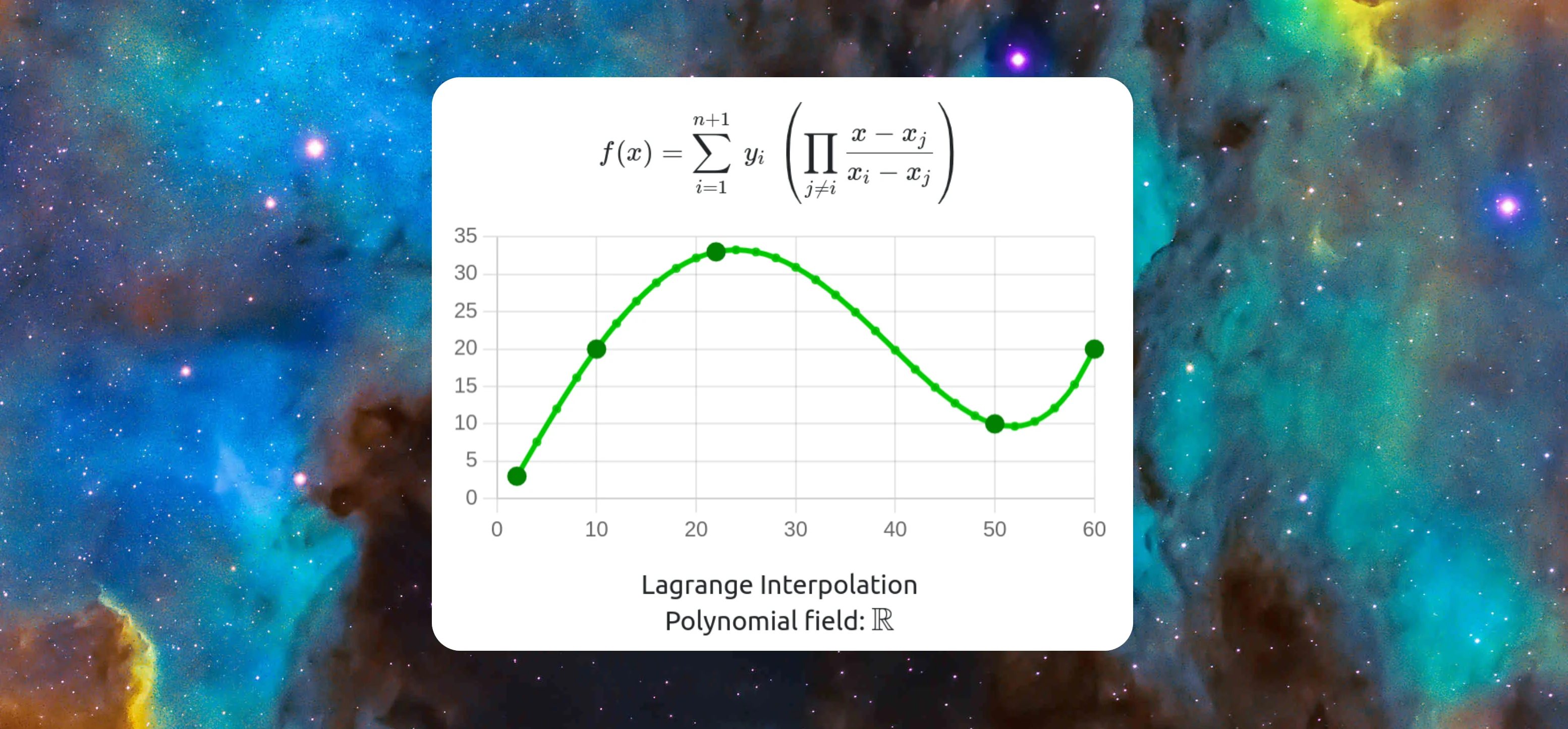
Los polinomios tienen una propiedad importante:
Para cualquier entero y cualquier lista de puntos en con , existe un único polinomio de grado como máximo tal que para todo .
Por ejemplo, si tenemos los puntos [2,3], [4,5], [5,2], [7,10], existe un único polinomio de grado 4 que pasa por ellos.
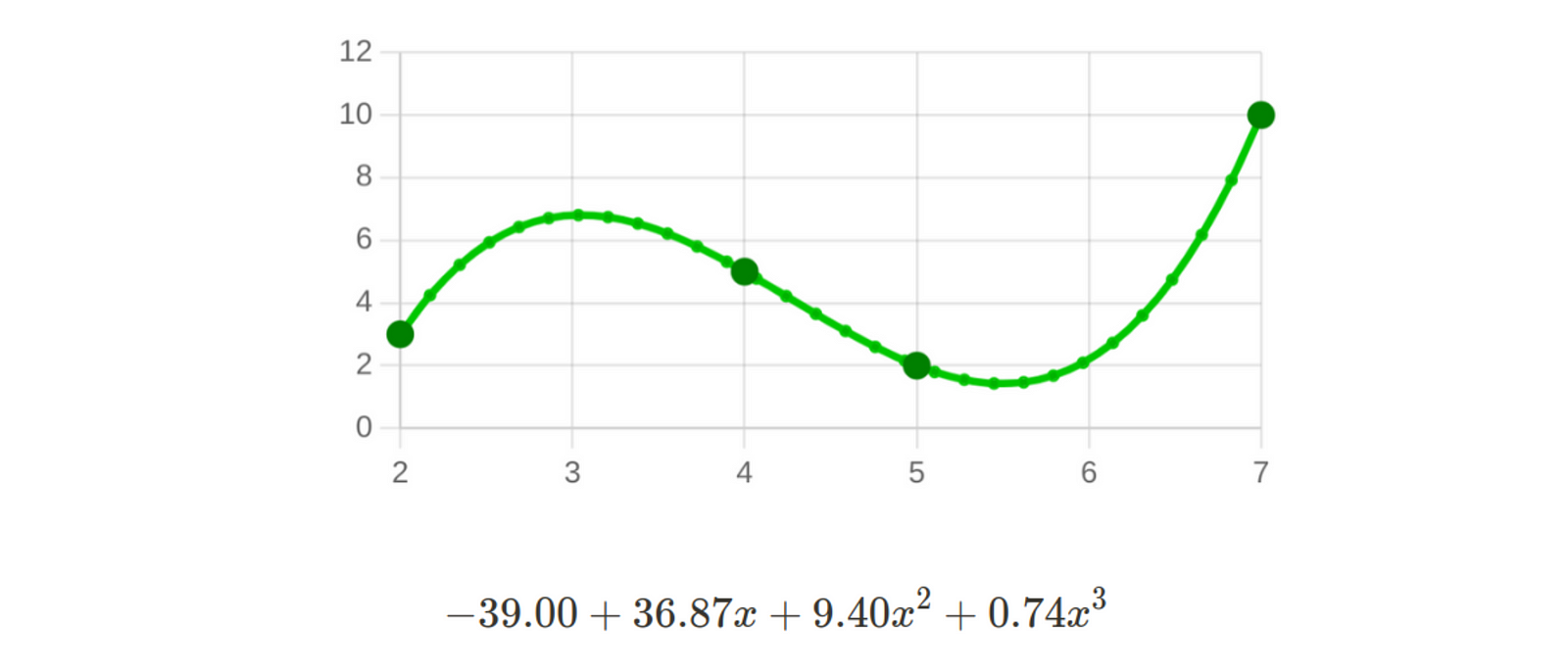
Hay varios métodos para obtener este polinomio, siendo los más conocidos el método de Lagrange y el método de Newton.
La clave es que, como describe Shamir, esta propiedad puede usarse para compartir un secreto de forma segura entre varias personas.
Supongamos que queremos compartir un secreto entre 7 personas, pero queremos que sólo se necesiten 5 de ellas para reconstruirlo. Hacemos lo siguiente:
- Generamos un número secreto:
- Creamos un polinomio aleatorio de grado 4 tal que :
- Calculamos los siguientes valores:
| ID | Valor |
|---|---|
| 1 | 882 |
| 2 | 731 |
| 3 | -2586 |
| 4 | -13251 |
| 5 | -37366 |
| 6 | -82953 |
| 7 | -159954 |
Con cualquier combinación de 5 de estos valores se puede recuperar el secreto evaluando el polinomio en .
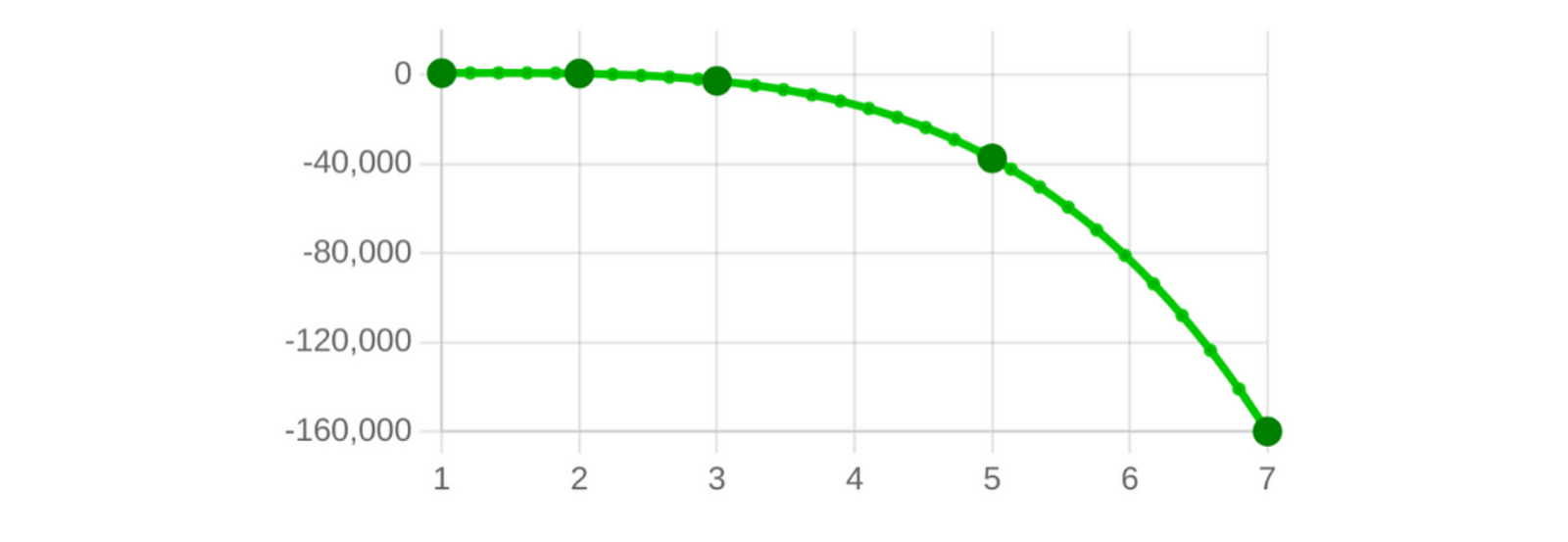
Este mecanismo es simple y potente. Aunque aquí hablamos de números, cualquier tipo de información puede codificarse numéricamente y compartirse de esta manera.
Aplicación web
Crear la aplicación web fue un desafío hermoso. Ya tenía conocimientos de Node, React y programación en general, pero nunca había hecho un proyecto de principio a fin por mi cuenta. Aprendí muchísimo en el proceso.
El repositorio está disponible en GitHub.
Empecé creando una API en Node con endpoints como uno que recibe un array de puntos y devuelve el polinomio correspondiente usando interpolación de Lagrange:
// Función en campo real
const lagrangeInterpolationFieldReal = (points) => {
let baseSum = new Polynomial([0], "float");
for (let i = 0; i < points.length; i++) {
let baseProd = new Polynomial([1], "float");
for (let j = 0; j < points.length; j++) {
if (i !== j) {
let term = new Polynomial([-points[j][0], 1], "float");
term = term.mul(
new Polynomial([1 / (points[i][0] - points[j][0])], "float")
);
baseProd = baseProd.mul(term);
}
}
baseSum = baseSum.add(
baseProd.mul(new Polynomial([points[i][1]], "float"))
);
}
return baseSum;
};Pero como explica Shamir, lo ideal es trabajar en campos finitos (modular), no con números reales. Eso mejora precisión y seguridad.
Esto evita aproximaciones y hace más eficiente el cálculo.
Aquí tienes la versión usando aritmética modular:
// Interpolación Lagrange con módulo
const lagrangeInterpolationFieldModP = (points, prime) => {
points = points.map((point) => [BigInt(point[0]), BigInt(point[1])]);
prime = BigInt(prime);
let baseSum = new Polynomial([0n], "bigint");
for (let i = 0; i < points.length; i++) {
let baseProd = new Polynomial([1n], "bigint");
for (let j = 0; j < points.length; j++) {
if (i !== j) {
let term = new Polynomial([-points[j][0] % prime, 1n], "bigint");
term = term.mul(
new Polynomial(
[
modDivide(
1n,
((points[i][0] % prime) - (points[j][0] % prime)) % prime,
BigInt(prime)
),
],
"bigint"
)
);
term = term.mod(prime);
baseProd = baseProd.mul(term);
baseProd = baseProd.mod(prime);
}
}
baseSum = baseSum.add(
baseProd.mul(new Polynomial([points[i][1] % prime], "bigint")).mod(prime)
);
baseSum = baseSum.mod(prime);
}
return baseSum;
};
const modDivide = (numerator, denominator, p) => {
const denominatorModP = ((denominator % p) + p) % p;
const inverse = modInverse(denominatorModP, p);
const result = (numerator * inverse) % p;
return (result + p) % p;
};
const modInverse = (num, p) => {
const [gcd, x, y] = extendedEuclidean(num, p);
if (gcd !== 1n) {
throw new Error("The multiplicative inverse does not exist in modulo p.");
}
const result = ((x % p) + p) % p;
return result;
};
const extendedEuclidean = (a, b) => {
if (b === 0n) {
return [a, 1n, 0n];
}
const [gcd, x1, y1] = extendedEuclidean(b, a % b);
const x = y1;
const y = x1 - ((a / b) | 0n) * y1;
return [gcd, x, y];
};Luego creé una interfaz con tres botones:
- Generar Secreto: permite ingresar el número de personas y el umbral de recuperación, y descarga un Excel con los valores.
- Descifrar Secreto: carga el Excel con los fragmentos y reconstruye el secreto.
- Limpiar Secreto: borra el valor guardado.
Después lo amplié con autenticación Google OAuth 2.0 y base de datos MongoDB Atlas para hacerlo multiusuario.
También creé un “Playground de Interpolación” donde los usuarios pueden experimentar con Lagrange y Newton en números reales o módulo primo.
Por ejemplo:
- Puntos: [2, 3], [10, 20], [22, 33], [50, 10], [60, 20]
- Primo: 1000000000039
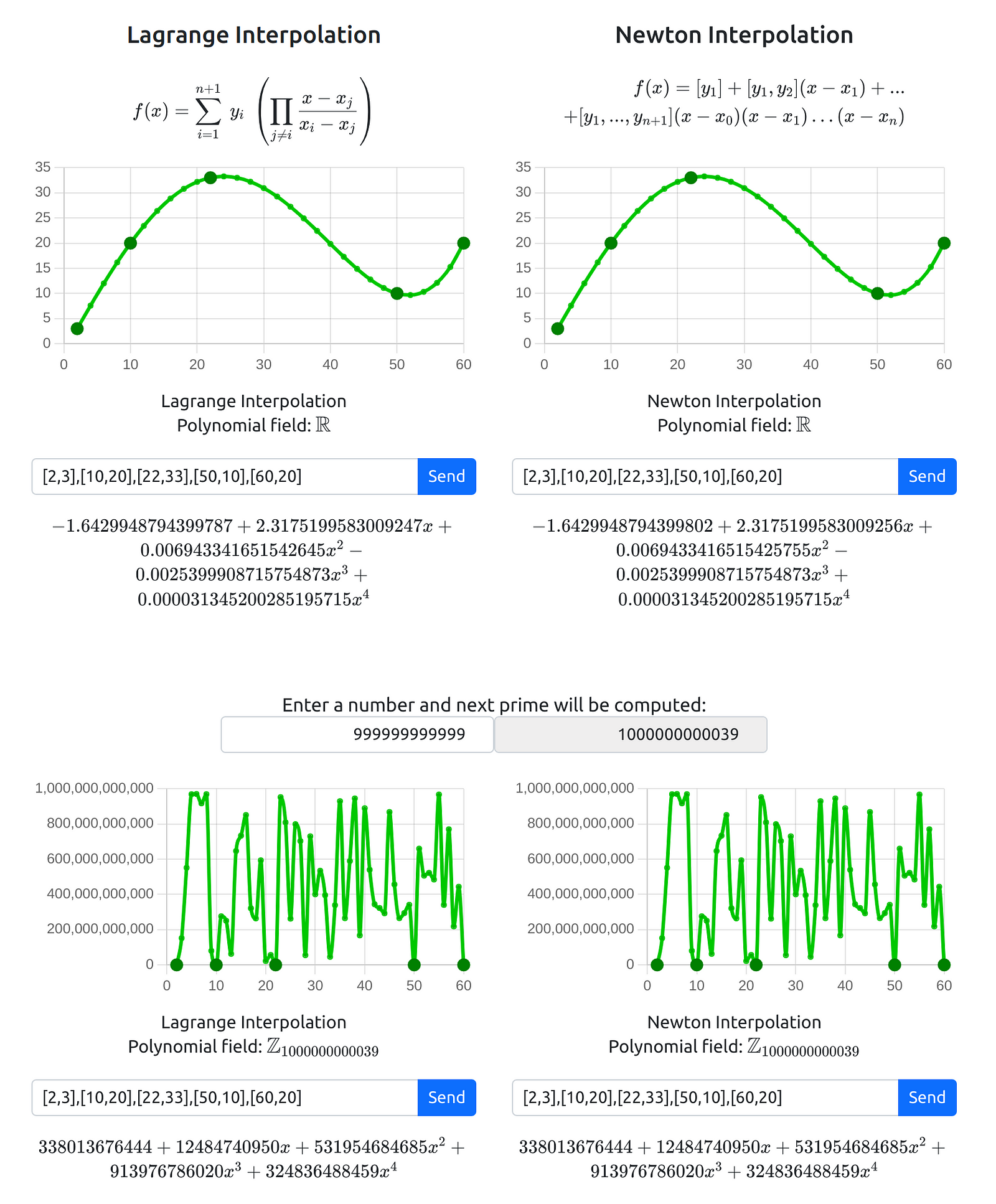
Como se ve, los resultados son equivalentes, pero en números reales hay decimales y errores de redondeo. En módulo primo, los resultados son exactos y controlados.
¿Te gustó esta historia? Puedes conectarte conmigo en LinkedIn o dejarme tus comentarios. ¡Gracias por leer!